Le théorème d'Archimède
Extrait du livre
La dérivation des fonctions est un concept universel qui offre tout à la fois une compréhension fine des courbes et une mise en évidence de liens insoupçonnés entre notions a priori très différentes. Le théorème d’Archimède en donne un bel exemple. Archimède, qui vivait à Syracuse au IIIe siècle avant J.-C., est l’un des plus grands savants de tous les temps. Il est connu du grand public pour la poussée qui porte son nom et le célèbre « Eurêka » qui aurait ponctué cette découverte. Esprit universel, à la fois astronome, ingénieur et géomètre, il est à l’origine de nombreuses découvertes dont les plus marquantes sont la vis sans fin, le principe du miroir ardent et un calcul révolutionnaire pour l’époque des décimales du nombre π. Mais son résultat le plus remarquable est la mise en lumière d’une correspondance cachée entre la sphère et le cylindre qui l’entoure. Cette correspondance établit en particulier l’égalité entre l’aire de la sphère et celle de son cylindre circonscrit : c’est le théorème d’Archimède.
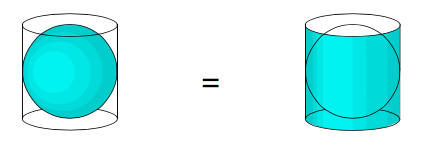
Au premier abord il peut paraître facile de vérifier le théorème d’Ar- chimède, il suffit de calculer l’aire de la sphère et celle du cylindre et de constater qu’elles sont égales. Pour le cylindre, qui n’est autre qu’un rectangle refermé sur lui-même, ce calcul d’aire ne pose pas de réel problème; en revanche pour la sphère il se révèle d’une grande difficulté tant conceptuelle que pratique. En effet, contrairement à certaines figures comme le cylindre ou le cône, la sphère ne peut se dérouler sur le plan, on ne peut donc calculer son aire comme si il s’agissait d’un objet plat. C’est là un obstacle important : la sphère est irréductiblement un objet de l’espace et diffère en cela radicalement du cylindre ou du cône. Comment, face à cette difficulté, accéder à son aire ?
Une observation très concrète va permettre de contourner cet obstacle : il est paradoxalement plus facile de mesurer un volume qu’une aire. En effet, pour accéder au volume d’un objet, il suffit de l’immerger dans un récipient gradué et d’observer la variation du niveau de l’eau et d’en déduire le volume recherché.

Comment obtenir l'aire de la sphère à partir de son volume ?
Tout repose sur la détermination d’une fonction f qui donne le volume d’une couche de peinture selon son épaiseur. On commence donc par recouvrir une sphère de rayon 1 d’une couche de peinture d’épaisseur x .
Comme le volume d’une couche de peinture recouvrant une surface donnée dépend évidemment de l’épaisseur x de cette couche, la fonction recherchée n’est autre que celle qui donne ce volume en fonction de l’épaisseur. Très précisément, si l’on désigne cette fonction par f , l’aire de la surface s’obtient alors en deux temps : on détermine tout d’abord la dérivée f ′, on remplace ensuite x par zéro dans cette dérivée. Le nombre que l’on trouve n’est autre que l’aire recherchée.
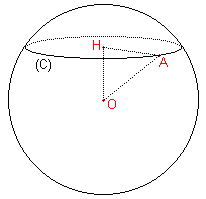
Calcul de l'aire d'une calotte sphérique