Le calcul intégral
Extrait du livre
En 1593, l’ambassadeur de Hollande Adrien Romain fut reçu par le roi Henri IV en son palais de Fontainebleau. Il affirma publiquement que la France ne comptait aucun grand mathématicien, le roi fit alors appeler un de ses conseillers qu’il savait féru de mathématiques : François Viète. L’ambassadeur, qui persistait dans son opinion, lança à ce dernier un défi. Saurait-il résoudre une équation du 45e degré si complexe qu’une seule page ne suffisait pas, selon la formulation de l’époque, à la contenir ? Il fallut moins d’un jour à Viète qui est aujourd’hui considéré comme le fondateur de l’algèbre moderne, pour résoudre cette équation. Beau joueur, Romain reconnut la grande valeur du mathématicien français et devint son ami. Au delà de son caractère pittoresque sans doute quelque peu accentué dans la narration de l’auteur qui l’a transcrite, Tallémant des Réaux, cette anecdote est révélatrice d’une pratique alors très courante, celle de se lancer des défis mathématiques. Il s’agissait de se mesurer au reste de la communauté en leur adressant des questions que l’on avait soi-même résolues et en les dotant généralement d’une forte somme d’argent.
En 1658, un personnage célèbre, Blaise Pascal, lance un défi qui met en jeu, d’après le mot de son auteur, la courbe la plus naturelle après la droite et le cercle. Malgré la très forte somme d’argent promise au vainqueur, personne ne réussit à résoudre la collection de problèmes proposés dans le délai imparti. Quelle était donc cette courbe? C’est celle que dessine un point situé au bord d’un disque qui roule sur l’horizontale : la célèbre cycloïde déjà rencontrée au premier chapitre.
Dans la vie de tous les jours, on peut observer une telle courbe en suivant du regard une lumière fixée sur la roue d’un vélo. Cette courbe a suscité l’intérêt des mathématiciens car elle est issue d’une combinaison très naturelle du cercle et de la droite. En dépit de sa simplicité, elle avait été ignorée par les Grecs et ne fut remarquée qu’au début du XVIIe siècle. Cette courbe étant toute nouvelle, ses propriétés restaient à défricher, à commencer par la question de l’aire. Celle d’un disque est bien connue, elle vaut πR2, mais quelle est la formule qui donne l’aire située sous une arche de cycloïde ? Cette question s’avéra très difficile et c’est Roberval, un des grands mathématiciens de l’époque, célèbre en outre pour la balance qui porte son nom, qui découvrit cette fameuse formule. Elle s’écrit 3πR2 : l’aire d’une arche est donc le triple de celle du disque qui l’engendre. Quant au défi de Pascal, il s’agissait d’une collection de nombreux problèmes toujours sur ce même thème de la cycloïde.
Comme on le constate avec les défis de Roberval et de Pascal, le calcul des aires était une question centrale qui préoccupait les plus grands es- prits de l’époque. Cette question va connaître une avancée spectaculaire avec l’apparition des principes du calcul intégral, un calcul dont l’émer- gence n’a été possible qu’avec la découverte préalable du calcul différentiel par Newton et Leibniz. Avec ces nouveaux principes, on a pu clarifier puis simplifier considérablement toutes ces questions de calcul d’aire au point qu’aujourd’hui les défis de Roberval et de Pascal sont à la portée d’un lycéen de classe de terminale, les calculs ne requérant que quelques lignes. Dans le cadre de la question de Kakeya qui porte justement sur l’aire des figures, ces mêmes principes s’appliqueront tout naturellement et rendront accessibles un grand nombre de figures nouvelles. Jusqu’à présent, les figures rencontrées sont en effet en nombre très restreint, une petite rétrospective en livre les principales : en premier lieu le disque dont l’aiguille est le diamètre, puis le Reuleaux et le triangle et enfin les différentes familles d’hélices.
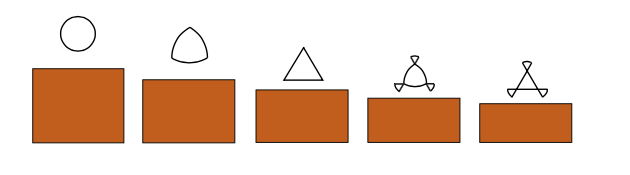


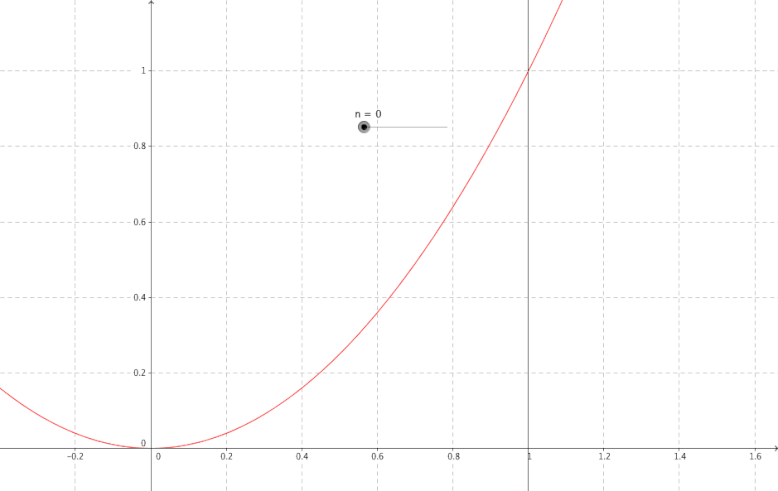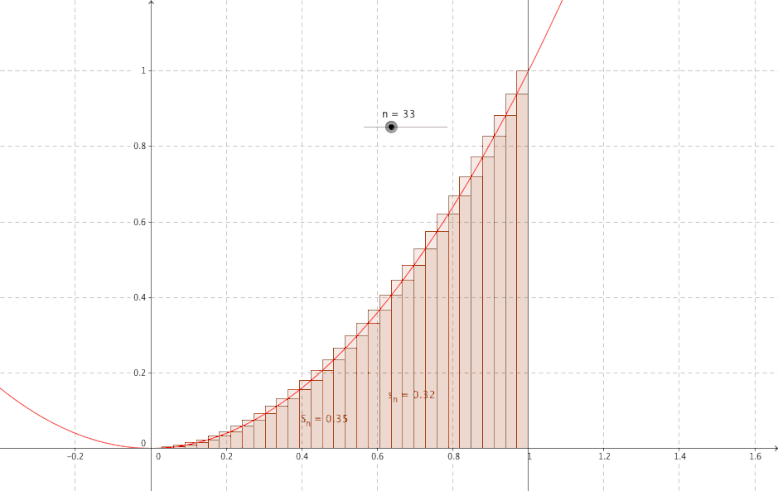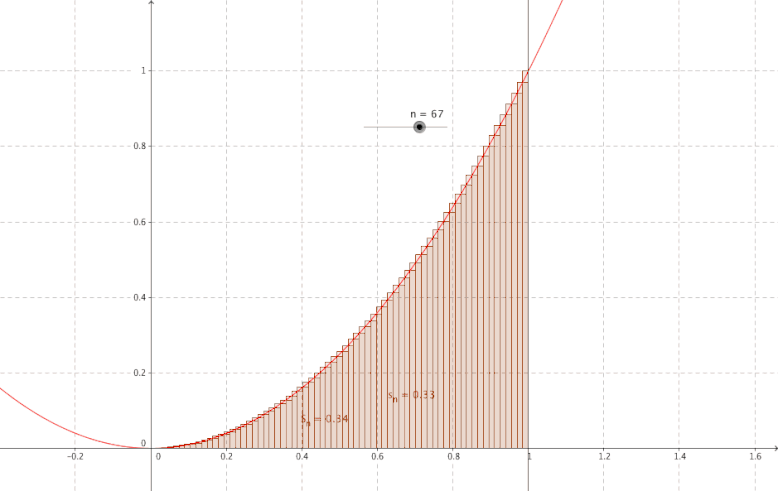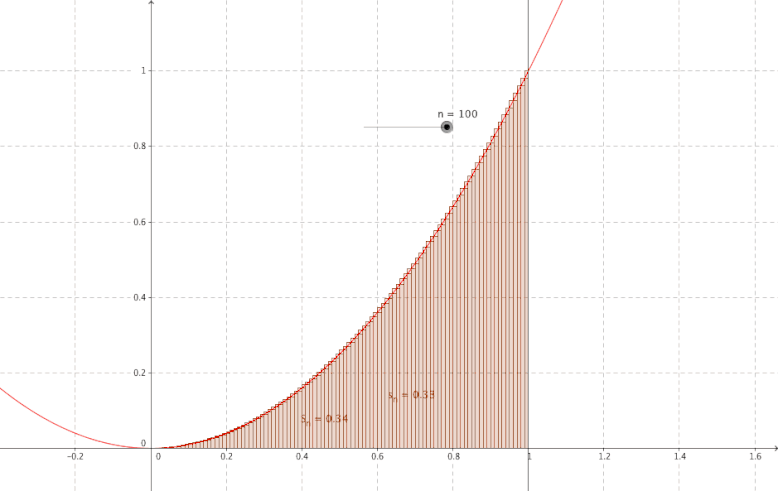
Comment obtenir l'aire d'une surface située sur une parabole ?