La découverte de Descartes
Extrait du livre
Reste qu’ici encore on se trouve confronté au problème de l’infini. En effet, la courbe des aires se compose d’une infinité de points et il faudrait calculer une infinité de pentes afin de déterminer exactement l’endroit où celle-ci vaut zéro. C’est maintenant que la grande invention de Leibniz et Newton entre en scène : la fameuse fonction dérivée. C’est elle qui, en effectuant l’ensemble infini des calculs de pente d’un seul coup, va permettre de surmonter cette difficulté. En effet, cette fonction dérivée embrasse à elle seule toutes les pentes en tous les points de la courbe ; en particulier, elle donne accès aux points précis où cette pente s’annule. À quoi pourrait bien ressembler une « fonction » capable d’une telle prouesse ? Concrètement, elle se présente comme une expression mathématique, c’est-à-dire une formule faisant intervenir une inconnue x et différents symboles mathématiques. On passe donc d’un problème purement géométrique, un problème de courbe et de pentes, à une formule contenant une inconnue. La clef de ce passage tient à l’existence d’un lien caché entre les objets géométriques et les formules mathématiques.
La découverte de Descartes
La mise en évidence de ce lien caché est l’œuvre de René Descartes et elle est aujourd’hui considérée comme l’une des plus grandes décou- vertes de l’histoire des sciences. Pourtant au début du XVIIe, Descartes lui-même n’accorde que peu d’importance à celle-ci, elle représente un outil pour résoudre tous les problèmes géométriques hérités de la géométrie des anciens. Il faut dire que le projet de Descartes est démesuré : il s’agit de construire rien moins qu’une mathesis universalis, une mathématique universelle qui étendrait son pouvoir à tous les domaines de la connaissance humaine. La réalisation de ce projet va occuper une grande partie de sa vie et aboutira, entre autres, à la rédaction du Discours de la méthode. Plus prosaïquement, il est à l’origine de la notation x , y et z pour les quantités inconnues d’une équation. Il a aussi considérablement simplifié les notations algébriques en introduisant en particulier la notation des puissances et en éliminant toutes sortes de symboles compliqués et redondants tirés des alphabets grec et hébreu. Sous son influence, l’écriture des expressions mathématiques devient plus cohérente et somme toute assez proche de celle que l’on utilise aujourd’hui : des nombres, des lettres de l’alphabet latin et des opérations algébriques comme la racine carrée. Bien sûr, l’œuvre de Descartes ne se limite pas à la science, il fait partie de ces savants à l’esprit universel qui se passionnent aussi bien pour l’optique, l’anatomie ou l’astronomie que pour la philosophie ou la théologie. Il se consacre d’ailleurs pleinement à toutes ses recherches et s’ingénie à fuir les mondanités qui l’en éloignent. Il mène une vie itinérante commencée à l’âge de 20 ans en s’engageant comme gentilhomme volontaire dans l’armée hollandaise. Il conserve toute sa vie ce goût de la mobilité puisqu’on le trouve en l’espace de quelques années résidant en Italie, à Paris, en Bretagne puis de nouveau en Hollande où il s’installe successivement à Franeker, à Amsterdam, à Leyde, à Deventer, à Sandport, à Hardenwijk, à Endegeest et à Egmond de Hoef ! Il meurt à Stockholm auprès de la reine Christine à l’âge de 53 ans.
Dans le domaine des sciences, l’apport le plus fondamental de René Descartes demeure sans conteste la célèbre géométrie algébrique, qui met en correspondance les courbes géométriques et les équations algébriques. Descartes commence par remarquer qu’une équation algébrique entre deux variables définit une courbe que l’on construit point par point. Chaque point, peut être repéré par deux nombres qui sont ses coordonnées sur chacun des deux axes, l’un et l’autre étant reliés par une formule.
Calcul de l'aire minimale

Calcul de l'aire d'une hélice faite avec un triangle de Reulaux
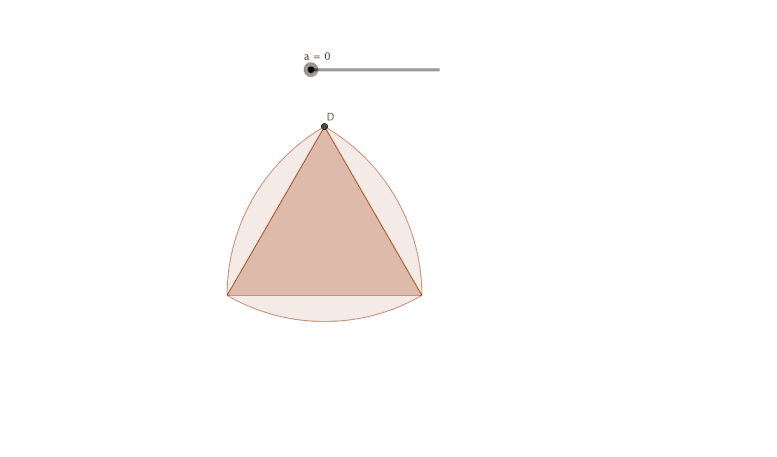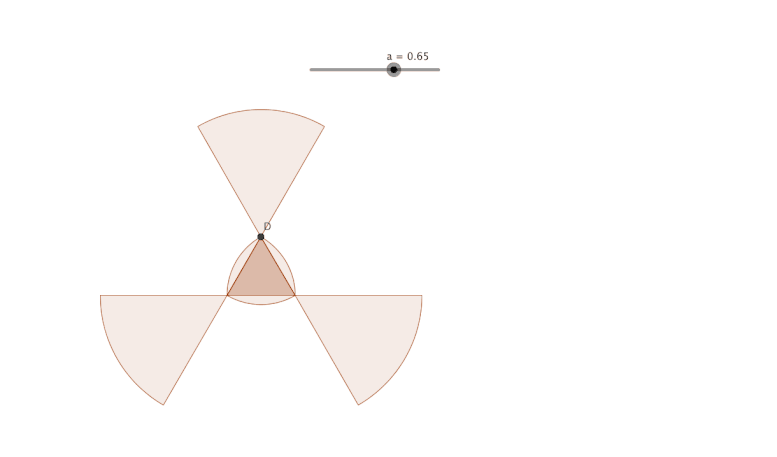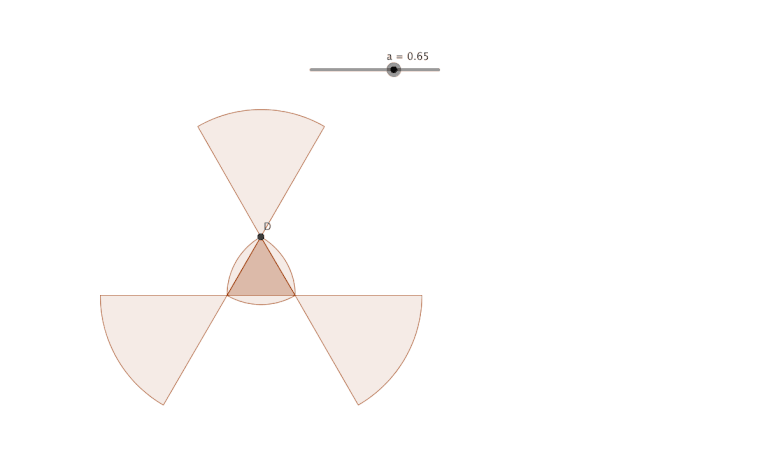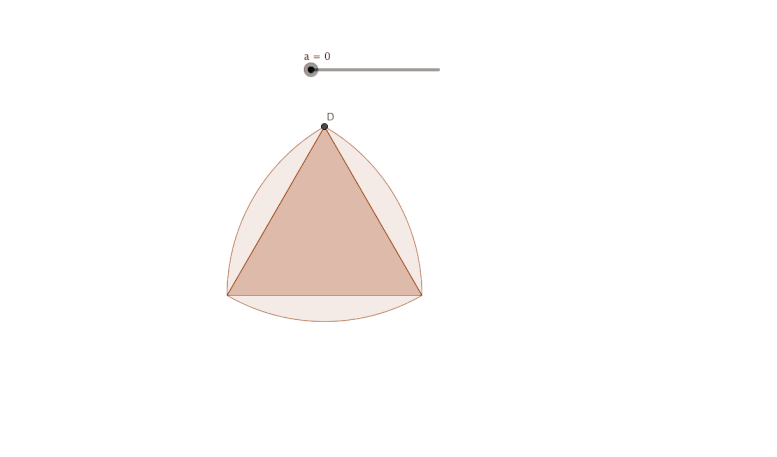
Calcul de l'aire d'une hélice faite avec un triangle équilatéral