Le paradoxe du peintre
Extrait du livre
Peut-on peindre un mur infini avec un nombre fini de pots de peinture ? Aussi surprenant que cela puisse paraître, la réponse est oui, c’est le célèbre paradoxe du peintre : il est possible de construire un mur dont la longueur est infinie et dont l’aire est finie. Ainsi, un peintre qui recouvri- rait ce mur d’une couche de peinture uniforme n’aurait besoin que d’un nombre fini de pots de peinture. Comment cela est-il possible ? La clé du paradoxe tient dans le fait que la hauteur de mur n’est pas constante mais va en s’amenuisant. Par conséquent, plus le peintre se déplace vers la droite, moins il a besoin de peinture pour couvrir une même longueur de mur. Cela dit, il faut garder à l’esprit que le mur est infini, et même si l’on a besoin d’une quantité de peinture de moins en moins grande, il reste tout à fait surprenant qu’au total une quantité finie de peinture soit suffisante.
Le secret de ce mur paradoxal réside précisément dans la manière dont il s’amenuise car il y a de nombreuses façons de construire un mur de plus en plus petit mais seules quelques unes d’entre elles conduisent à une aire globale finie. En mathématicien, on peut voir le mur comme un domaine délimité par la courbe d’une fonction, il s’agit alors de choisir une « bonne » fonction afin que la surface du mur soit finie. Bien entendu, il y a une multitude de fonctions qui revêtent une telle apparence et la réalisation ou non de ce mur paradoxal va dépendre de la fonction que l’on choisit. L’un des choix les plus simples que l’on puisse faire est de prendre la fonction l’inverse du carré, c’est-à-dire celle dont l’expression s’écrit f =1/x^2 . Le dessin ci-dessous en donne sa courbe représentative et le mur correspondant.
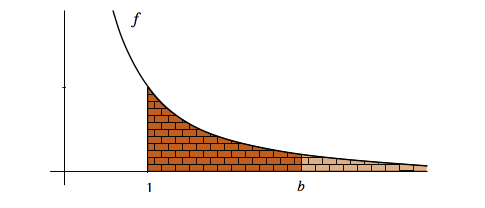
Comment obtenir l'aire de ce mur ?
La somme de tous les inverses n'a pas une somme finie.

