La formule de Stokes
Extrait du livre
De nos jours, où le savoir est plus largement partagé, les origines sociales des mathématiciens se sont bien diversifiées et l’appartenance ou non à la grande aristocratie n’est plus réellement un critère déterminant. On assiste d’ailleurs à un renversement de situation avec l’anoblissement dans certains pays des grands mathématiciens. Ainsi Andrew Wiles qui est parvenu à démontrer le très fameux théorème de Fermat a été nommé chevalier de l’Empire britannique en l’an 2000 par la reine d’Angleterre ! Parmi les prédécesseurs de Wiles, il en est un dont le nom reviendra souvent dans ce chapitre, il s’agit de Stokes, celui-là même qui a donné son nom à la très célèbre formule de Stokes. Georges Stokes est issu d’une famille relativement modeste d’Irlande, son père était pasteur et sa mère, fille de pasteur. Après des études brillantes, il ne tarde pas à devenir l’un des plus grands physiciens du Royaume-Uni. Et tout comme Wiles, il fut anobli et devint ainsi en 1889 le baronnet Sir Georges Gabriel Stokes.
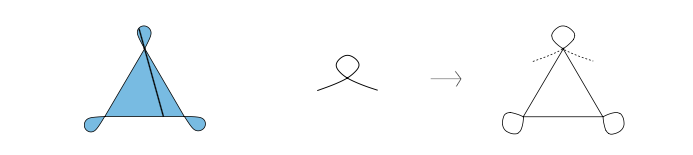
Que dit la fameuse formule qui porte son nom ? Elle donne un moyen direct et élégant pour connaître une aire à partir du contour qui englobe cette aire. En particulier elle est l’outil tout indiqué pour aborder le problème de Kakeya puisqu’elle permet non seulement de retrouver toutes les aires des figures qui sont apparues jusqu’à présent, mais elle donne également accès à l’aire de figures aux contours bien plus complexes. Cette formule, tout en se situant dans la veine du calcul intégral, en repousse les limites. L’intégration, en effet, ne s’applique qu’à des domaines très particuliers : ceux qui se situent au-dessous de la courbe d’une fonction. Or, dans la notion de courbe d’une fonction, il y a l’idée d’un déroulement sans retour en arrière.
La formule de Stokes offre un calcul direct de l’aire emprisonnée par une courbe qui se referme sur elle-même. Pour le problème de Kakeya, où l’on est sans cesse confronté à de tels domaines, c’est donc la formule idéale. Elle donne à celui qui chemine le long d’une telle courbe l’aire totale qu’il aura circonscrite en retrouvant le point de départ. Cette for- mule s’avère très intéressante d’un point de vue conceptuel puisqu’elle révèle toute la force du lien qui existe entre le contour et l’intérieur d’une figure. Elle donne un éclairage précis sur un fait qui est relativement in- tuitif : connaître le contour d’une figure, c’est connaître son intérieur.
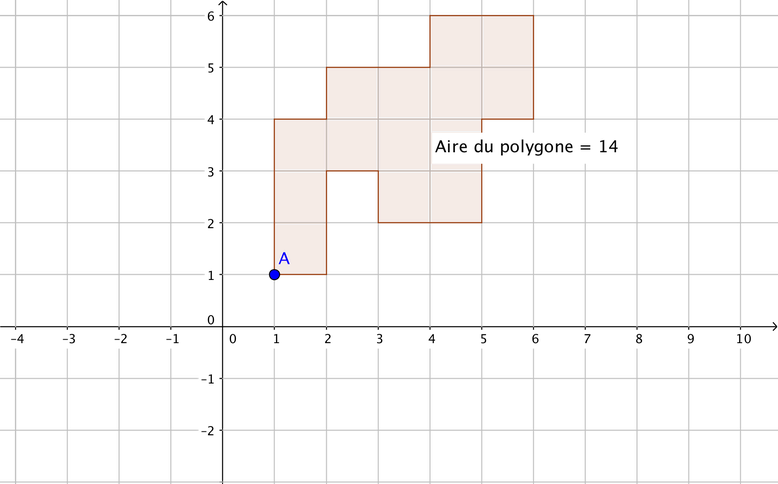
Méthode de l'arpenteur


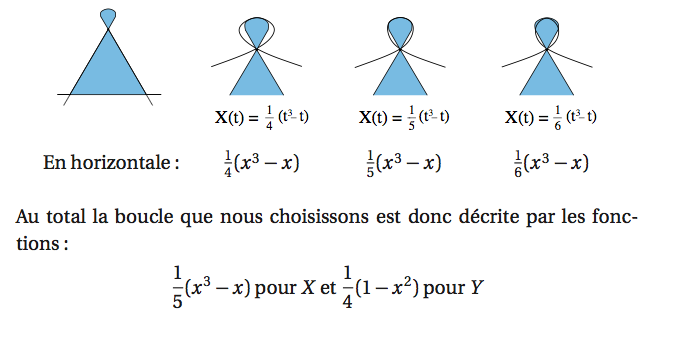
Calcul de l'aire de la boucle
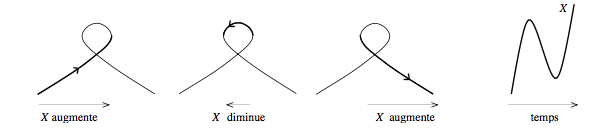
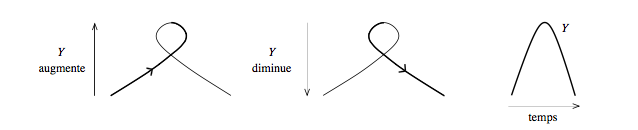

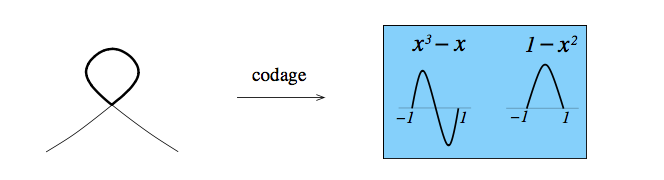

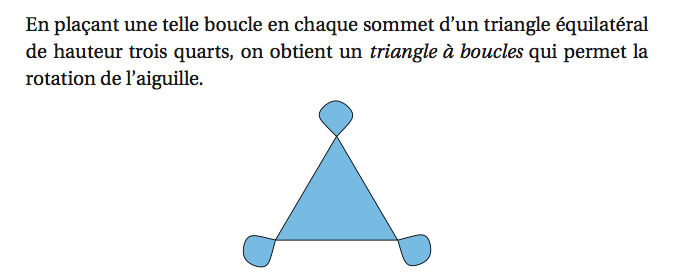
Calcul de l'aire d'un triangle à boucles